Magnetic Forces
Forces on Moving Charged Particles
If we run currents through two parallel wires, something unexpected
happens – the wires exert forces on each other! One might be inclined
at first to explain this by claiming that putting currents through the
wires puts electric charge into them, and that the electric charges are
exerting electrical forces on each other. But this is not correct.
Current is simply a steady flow of charge – there isn’t any charge
built-up in the wire. For every electron that enters the wire, a
corresponding electron exits it.
So the force must have something to do with the motion of the charges.
After further experimentation, we find that if we place a stationary net
charge near a conducting wire with current, there is no force between
them. So apparently there must be motion for both sets of charges in
order to exhibit this force.
While this force involves electric charge, it clearly is not electrical
in nature. That is, it is altogether different from the Coulomb force.
We therefore give it a different name... We call it the magnetic
force. Like the electric force, we will explain it in terms of a
vector field. And as with the electric force, this will require the
two-step theory of first explaining how a charge acts as a source for
the field, and then how another charge reacts to being in the presence
of a field.
We will approach this topic as if we were performing experiments to
extract the information we want. Here is a list of our observations from
these experiments:
-
The strength of the magnetic force on a charge is proportional to the magnetic field through which the charge is moving – This is not surprising, as it was also true for the electric force and field, but more to the point, it really is a result of our definition of magnetic field. \(\left|\overrightarrow F_B\right| \propto \left|\overrightarrow B\right|\)
-
The strength of the magnetic force on a charge is proportional to the magnitude of the charge – Again, not surprising. \(\left|\overrightarrow F_B\right| \propto q\left|\overrightarrow B\right|\)
-
The strength of the magnetic force on a charge is proportional to the speed at which the charge is moving though the field – This was mentioned above, and it is the first divergence form the electrical case. \(\left|\overrightarrow F_B\right| \propto q\left|\overrightarrow v\right|\left|\overrightarrow B\right|\)
-
The strength of the magnetic force on a charge varies depending upon the relative directions of the magnetic field and the charge’s velocity vector – Now this is new! Specifically, we find that the force is zero if the charge happens to be moving parallel to the field, and is its strongest when the field and velocity are perpendicular to each other. Further experimentation reveals that the strength of the force is proportional to the sine of the angle between the field and velocity vectors. \(\left|\overrightarrow F_B\right| \propto q\left|\overrightarrow v\right|\left|\overrightarrow B\right|\sin\theta\)
-
The direction of the magnetic force is perpendicular to both the direction of the velocity and the direction of the magnetic field – This is quite different from the electric case, for which the direction of the force and the field are always in the same or opposite directions. \(\overrightarrow F_B = q\overrightarrow v \times \overrightarrow B\)
Charge Motion in a Magnetic Field =================================
A charge within a magnetic field that is subject to no other forces
other than the magnetic force, follows a motion with a very interesting
property. The magnetic force only acts perpendicular to the direction of
motion, which means the charge can never speed up. Such a force can
only change the direction of motion. Why? If the force is always
perpendicular to the direction that the particle is moving, then this
force can never do any work, which means it can never cause a change in
the particle’s kinetic energy.
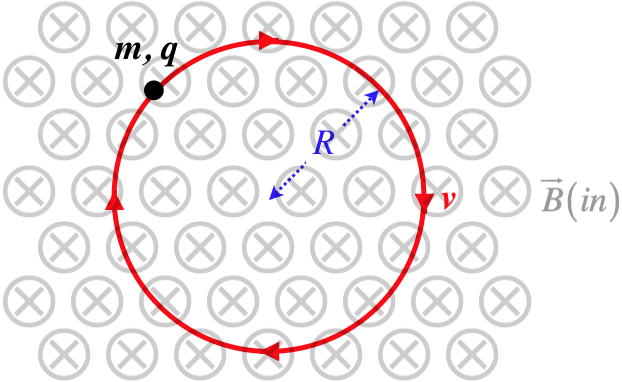
Let’s consider a simple case of a charged particle that moves in a plane
that is perpendicular to a uniform magnetic field. This charge would
experience a force that never changes magnitude (because the charge
remains unchanged, the field is uniform, the direction of the velocity
is always at right angles to the field, and as we stated above, it can’t
speed up. This constant-magnitude force is also always perpendicular to
the motion of the particle. These two conditions on the force (constant
magnitude and always at right-angles to the motion) sound very familiar
– these are the conditions for circular motion! Sure enough, such a
particle would move in a closed circle. We can use Newton’s 2nd law and
what we know about centripetal acceleration to put the magnetic force
together with the kinematic details of this particle’s motion.
Ignoring the sign of $q$ (i.e. treating it as an absolute value) we get: \(\overrightarrow F = m\overrightarrow a_c \;\;\;\Rightarrow\;\;\; qvB\sin 90^o = m\omega^2R \;\;\;\Rightarrow\;\;\; \omega = \dfrac{q}{m}B\) The angular speed of the particle depends only upon its charge, its mass, and the magnetic field strength.
Forces on Current-Carrying Wires
We have a vector equation describing the force on a point charge moving through a field, and now we would like to extend this result to currents flowing through conductors in a magnetic field. To do this, we use a common chain-rule trick to relate current through a short length of wire to a moving charge: \(I = \dfrac{dq}{dt} = \dfrac{dq}{dl}\dfrac{dl}{dt}\;\;\;\Rightarrow\;\;\; I\;dl = dq\dfrac{dl}{dt} = dq\;v\) If we take into account the direction of the current flow through $dl$ and the velocity, we have the vector version of the contribution of a small segment of current, and we can plug it into the force equation: \(I \;\overrightarrow {dl} = dq \;\overrightarrow v \;\;\;\Rightarrow\;\;\; d\overrightarrow F = dq \;\overrightarrow v \times \overrightarrow B = I \;\overrightarrow {dl} \times \overrightarrow B\) If the total force on a length of wire is desired, all the infinitesimal contributions to force need to be integrated. This can present a challenge is the wire is not straight, since $\vec dl$ changes direction, or, of course, if the magnetic field changes from one point of the wire to the next. In practice, we frequently deal with straight-line segments in uniform magnetic fields, which yields a simple result for the magnitude (the direction can be determined by the right-hand-rule): \(\text{force on straight wire of length } L \text{ and current } I \text{ in uniform field } B = ILB\)