Very Summarized Notes on Rotational Dynamics

Dynamics of Rotational Motion

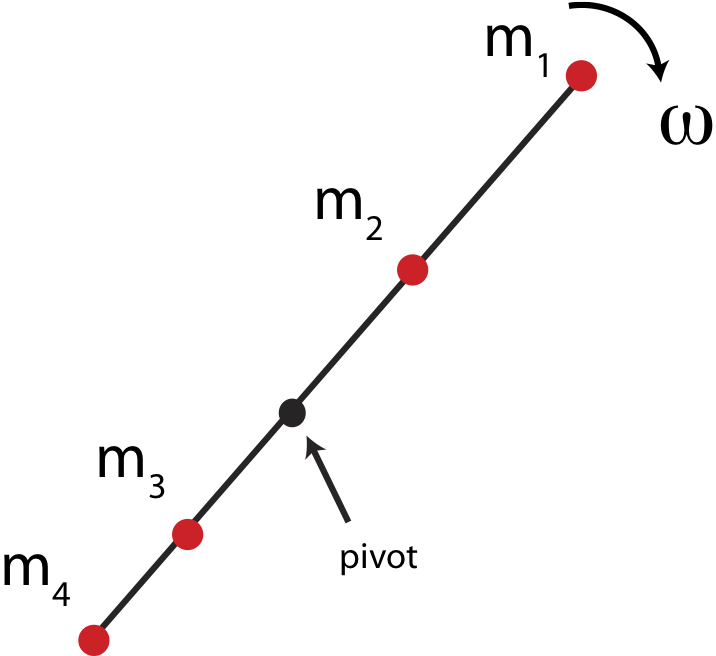
Rotational motion describes how an object rotates around an axis. It is essential for understanding various physical phenomena, from the motion of celestial bodies to the operation of mechanical systems. The pivot shown below defines a fixed point about which the object rotates. In some cases it is an obvious choice, such as in this example since we are assuming rod is held in place at a pilot.

In this scenario the total kinetic energy of the rotating object is the sum of the kinetic energies of the four masses shown. For mass 1, $m_1$ , we can write down the kinetic energy in terms of linear speed, and then use the relationship between angular and linear speeds, $v1=r_1\omega$, where $r_1$ is the distance from the pivot to the location of $m_1$ \(K=\frac{1}{2}m_1v_1^2=\frac{1}{2}m_1(r_1\omega)^2=\frac{1}{2}m_1r_1^2\omega^2\) The expression is similar for all the other masses, using the appropriate distances from the pivot and recognizing that all masses will rotate with the same angular velocity. The total kinetic energy for this rotating object would be the sum of all the individual kinetic energies: \(K=\sum_{i=1}^{4}\frac{1}{2}m_iv_i^2=\frac{1}{2}(m_1r_1^2+m_2r_2^2+m_3r_3^2+m_4r_4^2)\omega^2\) In general, for a set of N masses, the kinetic energy of a rotating object about a fixed pivot becomes: \(KE=\sum_{i=1}^{N}\frac{1}{2}m_iv_i^2=\frac{1}{2}\Big(\sum_{i=1}^{N}m_ir_i^2\Big)\omega^2\) We can write down the rotational analog of kinetic energy: \(K_{rot}\equiv\frac{1}{2}I\omega^2\) Comparing the expression for linear and angular kinetic energies, we see that rotational inertia is the rotational analog of mass. The rotational inertia of an object does not depend solely on the amount of mass in the object, but on how this mass is distributed relative to the axis of rotation.
In general, most objects are not made-up of point masses but are continuous mass. The sum we initially used to express moment of inertia can be turned into an integral in the limit of infinitesimally small mass increments when the mass becomes continuous: \(I=\int r^2 dm\) The rotational inertia of a composite object is the sum of the rotational inertias of each component, all calculated about the same axis. \(I_{total} = I_1 + I_2 + I_3 + \dots\)

Common Shapes

Different geometrical shapes have standard formulas for calculating moment of inertia: - Solid Cylinder (about its axis): \(I = \frac{1}{2} m r^2\) - Solid Sphere (about its center): \(I = \frac{2}{5} m r^2\) - Thin Rod (about center): \(I = \frac{1}{12} m L^2\) These formulas highlight the dependence of moment of inertia on both mass and the distribution of that mass relative to the rotation axis.

Further Reading

• Moment of Inertia using Integrals

Torque

Torque ($\tau$) is the rotational equivalent of linear force and measures how effectively a force causes an object to rotate about an axis. Now we want to develop the analog of the 2nd Law with will relate "rotational force", known as torque, $\vec \tau$, which will determine how angular motion will change. There is a fundamental difference between force and torque: specifically, not all forces will result in torques, and not all torques will results in net forces. Since rotational inertia is analogous to mass, and angular acceleration is analogous to linear acceleration, we can write down the analog of Newton’s 2nd Law: \(\tau=I\alpha\) Focusing on magnitude only for now and applying Newton’s 2nd Law for linear motion to the mass and using the connection between linear and angular acceleration, $a=r\alpha$, we can deduce the following (at least, for a point mass) \(F=ma \implies F=mr\alpha\) For a point mass, we know the moment of inertia is $mr^2$ \(\tau= mr^2\alpha \implies \tau= mr\alpha r= mar\) \(\tau= Fr\) For example, the pivot can represent a hinge of a door. The door swings back and forth about the hinge, and we apply forces to the door when we push it in order to open it. The further away from the door you push, the easier it is to open it since you are applying a greater torque simply by applying a force further from the hinge (pivot).

Definition and Calculation of Torque

The torque produced by a force $F$ acting at a distance $r$ from the pivot point is given by: \(\tau = r \times F\) In terms of its magnitude: \(\tau = rF \sin(\theta)\) where $\theta$ is the angle between the force vector and the lever arm.

- The unit of torque is Newton-meters (Nm), indicating that torque is a measure of force multiplied by distance.

Angular Momentum and Its Conservation

Angular momentum ($L$) is defined as the product of moment of inertia and angular velocity: \(L = I \omega\) If a system has many parts, its total angular momentum is the vector sum of the angular momenta of all the parts: \(L = L_1 + L_2 + L_3 \dots = \sum L_i\) For a system of particles or objects we can write a model for angular momentum: \(\textrm{Net external angular impulse}=\textrm{ang }\vec J_{net,ext} = \int\limits_{t_i}^{t_f} \sum \vec\tau_{ext} dt= \Delta\vec L_{\textrm{system}}\) The principle of conservation of angular momentum states that if no external torque acts on a system, the total angular momentum remains constant: \(L_{initial} = L_{final}\)

Implications of Conservation

This principle implies that if a rotating object decreases its moment of inertia (such as a skater pulling in their arms), its angular velocity must increase to conserve angular momentum. This behavior is crucial in various physical systems and phenomena. A system acted on by external torque undergoes a change in total angular momentum equal to the net angular impulse (total angular impulse) of the external torques. We can rephrase the relationship stated above as a conservation principle for the total angular momentum of a system of particles.

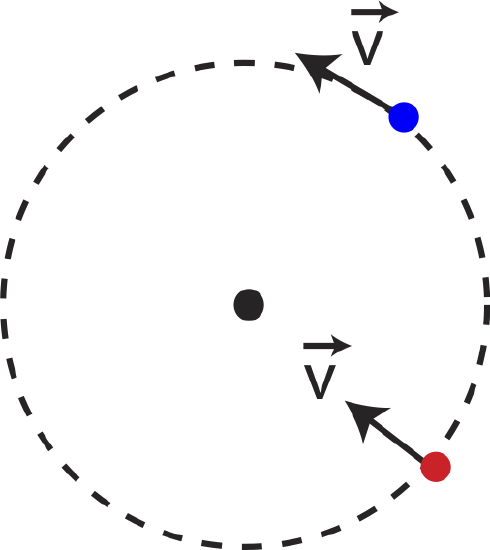
For a particle with mass, $m$, and speed ,$v$, the angular momentum can also be expressed as a function of the linear momentum: \(\vec L=I\vec\omega=mr^2\frac{\vec v}{r}=mr\vec v=r\vec p\) However, we consider the red particle instead, which is moving with the same speed but toward the center of the circle, it has no angular momentum relative to the center of the circle. Thus, even though the red particle has the same linear momentum as the blue one, it has zero angular momentum relative to the center of the circle, since there is no change in angle relative to the center. So, we can deduce that only the tangential component of the linear momentum matters. \(L=r\vec p_{\perp}\label{L-point}\) We also have seen multiple times before that, in such situations, the equations boils down to a simple cross product. \(\vec L=\vec r\times\vec p\)

Newton’s Universal Law of Gravitation

Newton’s law of gravitation states that every point mass attracts every other point mass with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them: \(F = G \frac{m_{1} m_{2}}{r^{2}}\) where: - $F$ is the gravitational force between two masses, - $G$ is the gravitational constant ($6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2$), - $m_1$ and $m_2$ are the masses, and - $r$ is the distance between the centers of the two masses.

Gravitational Force and Weight

The gravitational force can also be interpreted as the weight of an object, given by: \(W = mg\) where $g$ is the acceleration due to gravity ($9.81 \, \text{m/s}^2$ near the Earth’s surface). This relationship shows that weight is the force experienced by an object due to gravity.

Satellites and Kepler’s Laws

Satellites are objects that orbit a planet or star, and Johannes Kepler formulated three laws that describe their motion.

Kepler’s Laws of Planetary Motion

• Kepler’s First Law (Law of Ellipses): The orbit of a planet is an ellipse with the Sun at one of the two foci. This law highlights the elliptical nature of planetary orbits.

• Kepler’s Second Law (Law of Equal Areas): A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This means that a planet moves faster when it is closer to the Sun and slower when it is farther away.

• Kepler’s Third Law (Law of Harmonies): The square of the orbital period ($T$) of a planet is directly proportional to the cube of the semi-major axis ($a$) of its orbit: \(T^2 \propto a^3\)

Derivation of Kepler’s Third Law for Circular Orbits

For a circular orbit, the centripetal force required to keep a planet in orbit is provided by gravitational attraction: \(F = \frac{mv^{2}}{r} = G \frac{mM}{r^{2}}\) where $M$ is the mass of the central body (e.g., the Sun). Rearranging for the orbital velocity $v$: \(v = \sqrt{\frac{GM}{r}}\) The orbital period $T$ is related to the velocity: \(T = \frac{2\pi r}{v}\) Substituting for $v$ gives: \(T^2 = \frac{4\pi^2 r^3}{GM}\) This relationship shows that the square of the period is proportional to the cube of the radius of the orbit, confirming Kepler’s Third Law.

Download the notes as a PDF

To download and read a PDF version of the notes as a PDF, visit the link below

• physics.kebede.org/assets/notes/rot-dyn/notes.pdf